一.基本：二次函数一般式转顶点式

1.1理解二次函数一般式与顶点式

首先，我们要清楚二次函数的一般式是 y = ax^2 + bx + c，其中 a, b, c 是常数，并且 a ≠ 0，而顶点式是 y = a(x - h)^2 + k。

1.2转化步骤

0. 找出a, b, c的值： 从给定的二次函数一般式中，我们可以直接读出 a, b, c 的值。

1. 公式法求h的值： 顶点横坐标 x 的值可以通过公式 h = -b / (2a) 计算得出。这个公式是二次函数对称轴的公式，也是顶点横坐标的公式。

2. 公式法求k的值： 通过公式 k=(4ac-b^2) / (4a) 计算得出。这个公式是顶点纵坐标的公式。

3. 写出顶点式： 使用求得的 h 和 k 值，以及原一般式中的 a 值，写出二次函数的顶点式 y = a(x - h)^2 + k。

1.3注意事项

• 在计算过程中，注意确保分母 2a 不为零，即 a ≠ 0。

• 当 b^2 - 4ac 小于零时，二次函数没有实数根，但它仍然有一个顶点。

• 在代入和计算时，注意保持数学表达式的准确性，避免计算错误。

1.4在C语言中进行计算

#include <stdio.h>
​
int main() {
double a, b, c, h, k;
​
// 输入二次函数的一般式系数
printf("请输入二次函数的一般式系数 a, b, c: ");
scanf("%lf %lf %lf", &a, &b, &c);
​
// 计算顶点的 h 和 k
h = -b / (2 * a);
k = (4.0 a c - b b) / (4.0 a);;
​
// 输出顶点式与顶点
printf("二次函数的顶点式为:\n");
printf("y = %.2lf * (x - %.2lf)^2 + %.2lf\n", a, h, k);
return 0;
}

二.完善：反馈二次函数的顶点

2.1理解二次函数的顶点

在顶点式中， y = a(x - h)^2 + k其中 (h, k) 是二次函数的顶点坐标,也就是[-b/2a,(4ac-b^2)/(4a)]。

2.2反馈方法

printf("顶点坐标为：(%.2lf, %.2lf)\n", h, k);
//这个是由于我们在上一步早已经计算好了h，k的值

2.3最终代码

#include <stdio.h>
​
int main() {
double a, b, c, h, k;
​
// 输入二次函数的一般式系数
printf("请输入二次函数的一般式系数 a, b, c: ");
scanf("%lf %lf %lf", &a, &b, &c);
​
// 计算顶点的 h 和 k
h = -b / (2 * a);
k = (4.0 a c - b b) / (4.0 a);
​
// 输出顶点式与顶点
printf("二次函数的顶点式为:\n");
printf("y = %.2lf * (x - %.2lf)^2 + %.2lf\n", a, h, k);
printf("顶点坐标为：(%.2lf, %.2lf)\n", h, k);
return 0;
}

三.进阶：检测a是否为0，并报错

3.1理解二次函数的a不可以为0

如果a为0，则函数中二次项无意义，这不是一个有效的二次函数，无法计算k值。

3.2判定方法

使用if语句，如果a等于零，则报错，否则就正常运算。

if (a == 0){
printf("错误：a不可以等于0\n");
return 1;
// 返回非零值表示程序异常终止
}
else {
// 计算顶点的 h 和 k
h = -b / (2 * a);
k = (4.0 a c - b b) / (4.0 a);
}

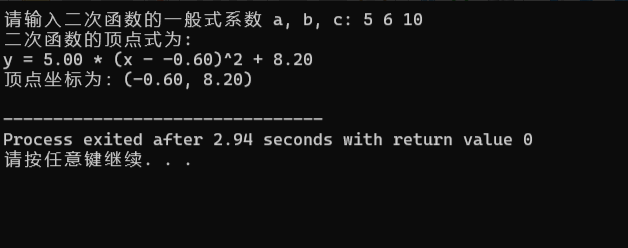
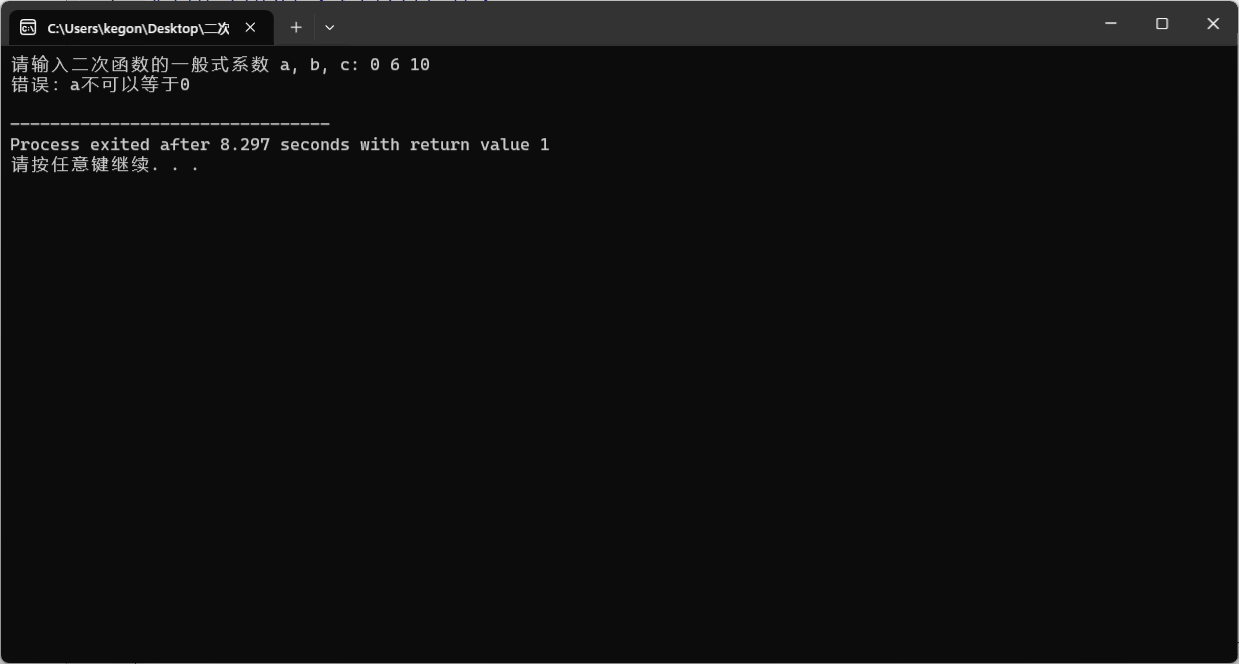
四.结束：完整代码与测试

#include <stdio.h>
​
int main() {
double a, b, c, h, k;
// 输入二次函数的一般式系数
printf("请输入二次函数的一般式系数 a, b, c: ");
scanf("%lf %lf %lf", &a, &b, &c);
// 检查 a 是否为零
if (a == 0) {
printf("错误：a不可以等于0\n");
return 1;
// 返回非零值表示程序异常终止
}
else {
// 计算顶点的 h 和 k
h = -b / (2 * a);
k = (4.0 a c - b b) / (4.0 a);
​
// 输出顶点式与顶点
printf("二次函数的顶点式为:\n");
printf("y = %.2lf * (x - %.2lf)^2 + %.2lf\n", a, h, k);
printf("顶点坐标为：(%.2lf, %.2lf)\n", h, k);
return 0;
}
}

四.附录：变量说明

0. a：一般式 y = ax^2 + bx + c 中二次项系数

1. b：一般式 y = ax^2 + bx + c 中一次项系数

2. c：一般式 y = ax^2 + bx + c 中常数项

3. h： y = a(x - h)^2 + k中的h，顶点坐标点一部分（具体计算过程见【1.2 转化步骤】）

4. k：y = a(x - h)^2 + k中的k，顶点坐标点一部分（具体计算过程见【1.2 转化步骤】）